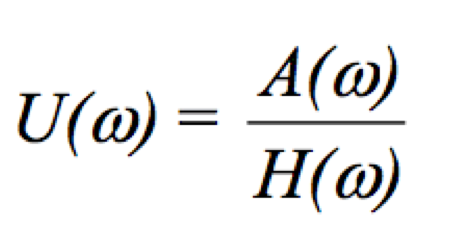Filter Correction

The uncorrected records collected by the recording instrument are generally processed for the following purposes:

a) correction with respect to the instrument characteristic curve;

b) correction of the high and low frequency errors;

c) filtering, in order to highlight or eliminate a particular frequency band.

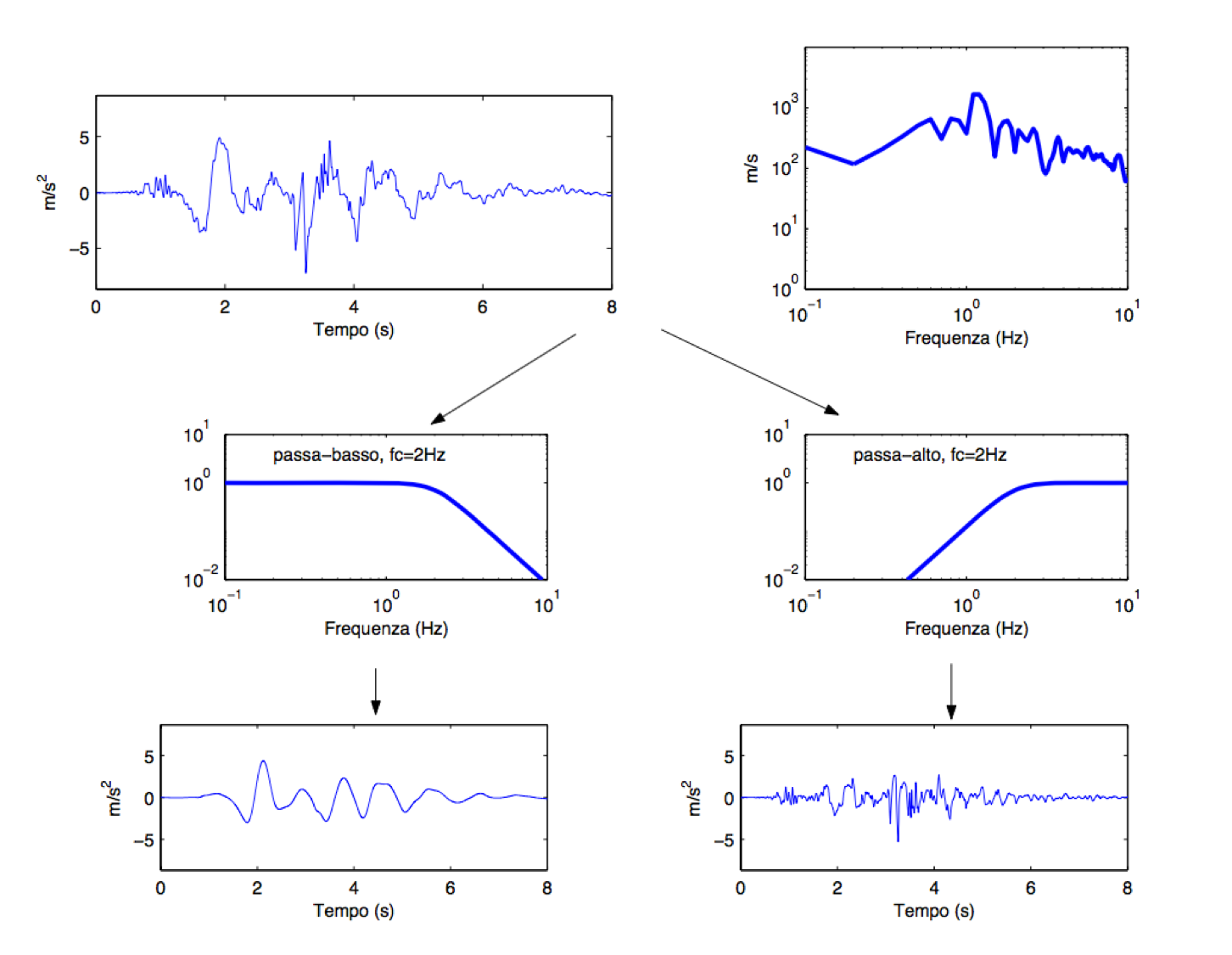
Example of the effect of filter application on an accelerometric signal. Top: EW component of the accelerogram recorded in Gemona del Friuli (GMN) the September 15th 1976 03:16, and corresponding Fourier spectrum. Bottom: the same accelerogram high-pass filtered (left) and low-pass filtered (right), in both cases with a corner frequency fc= 2Hz.^[1]

Such operations are often performed in the frequency domain, using filtering algorithms based on the Fast Fourier Transform (FFT), and schematized by the following procedure:

1. The FFT of the original accelerometric record is performed:

2. The instrument characteristic curve H(_) is removed. Recalling that A(_) = H(_)_U(_), the Fourier transform of the record is obtained, in which the instrument response is removed:

3. The filter is applied in the frequency domain by multiplying the function U(_) times the filter B(_), either high-pass, or low-pass or band-pass, depending on the type of disturbance to eliminate or of the frequency band to highlight:

4. The inverse Fourier transform is computed, to obtain the corrected signal in the time domain: